[Index][Previous-Solution][Next-Conclusion]
Evaluation
Verification
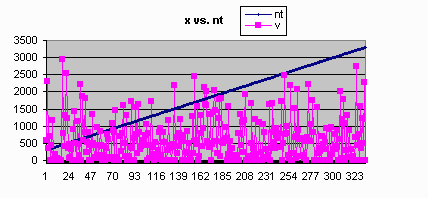
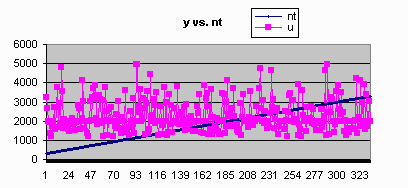
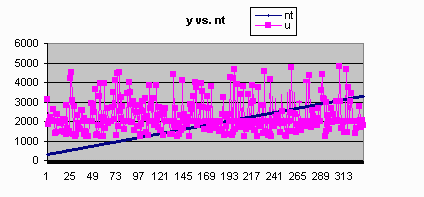
Since we broken the single-chain into multi-chain by broken some dependent relationships,
will it influence the sampling? And how big the influence will be? To varify whether or not
the duel chain works becomes important part in this section. The comparision is given between
the results generated by sequential Gibbs Sampler(single-chain) and the results generated by
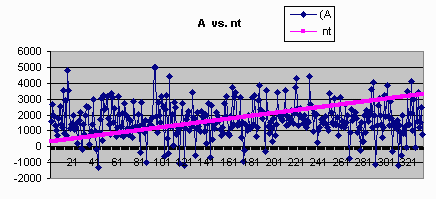
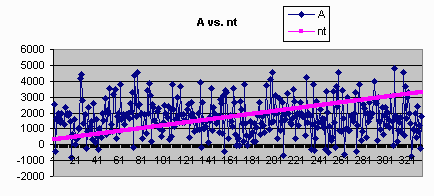
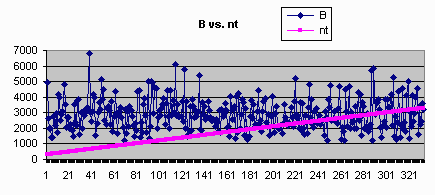
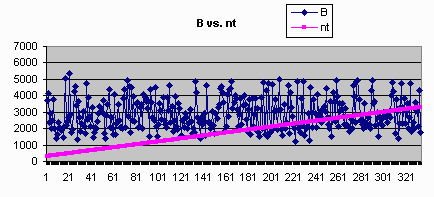
parallel Gibbs Sampler(duel-chain). We compared the average value of every single variable,
and the number of points that fall in the range of a fixed bound.
| Serial Result | Parallel Result | Mistake |
|---|
| Average A | 1685.33 | 1651.12 | 2.03% |
|---|
| Average B | 2885.60 | 2881.36 | 0.15% |
|---|
| Average x | 600.131 | 615.124 | 2.50% |
|---|
| Average y | 2285.47 | 2266.24 | 0.84% |
|---|
x - #point in (400,
2000)/#total points | 195/333 | 185/333 | 5.13% |
|---|
y - #point in (400,
2000)/#total points | 162/333 | 155/333 | 4.32% |
|---|
| Parallel Result | Serial Result |
|---|
 |
 |
|
 |

|
 |
|
 |
All the data calculated, collected and showed above are based on the Console
version of Parallel Gibbs sampler,
and the following parameters:
Initial x = 750, y = 200, High Bound = 2000, Low Bound = 400,
Burning = 1000, Iteration = 1000, Thinning = 3, Volumn of Data Set = 898.
Performance Evaluation
Performance evaluation is given by the comparision of the speed on the Sequential
Method and Parallel Method:
Volumn of
Data Set | Sequence |
Paralle Time(sec) | Serial Time(sec) | SpeedUp |
|---|
| 7520 | Nb = 1000
Nt = 1000 | 1.687 | 3.016 | 1.75 |
Nb = 2000
Nt = 3000 | 4.234 | 7.516 | 1.775 |
| 20000 | Nb = 1000
Nt = 1000 | 4.25 | 7.437 | 1.75 |
Nb = 2000
Nt = 3000 | 10.671 | 18.547 | 1.738 |
| 40000 | Nb = 1000
Nt = 1000 | 7.968 | 13.625 | 1.71 |
Nb = 2000
Nt = 3000 | 20.016 | 34.047 | 1.70 |
The data above is based on two variables-Gibbs Sampler. The ideal(maximun) SpeedUp = 2.0
Bingxue Cai
Send Comments to: bingxuec@cs.byu.edu







