Broken Algorithm (two variables case):
1. initiate both of two variables:
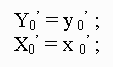
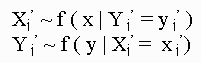 (4)
(4)3. make single chain (2) a duel chain
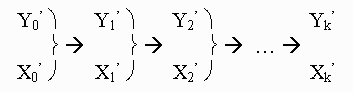 (5)
(5)[Index][Previous-Introduction] [Next-Evaluation]
As we can see, scalability is the biggest problem to Gibbs Sampler. Via single sequence (2), it is hard to parallel the algorithm, since the sampling for all variables are related to the the previous sample.
By breaking part of relationships in the sequence, we could achieve the goal of parallism. Here we introduce both the Broken Algorithm and the Parallel strategy for paralleling the Gibbs sampler.
Broken Algorithm (two variables case):
1. initiate both of two variables:
2. alternate generating values from:
(4)
3. make single chain (2) a duel chain
(5)
Multi-chain Parallism Strategy:
1. Using Broken Algorithm, we first break the "Gibbs sequence" from one single-chain to multi-chain depending on the number of the Integral's dimensions.
2. The functional decomposition strategy will be used in the following implementation. Let M be the Integral's dimension, we need at most M processors. Each processor will be responsible for one chain, which means each processor is responsible for one variable's computation.
3. At the end of each computation stage, the global communication will take place to exchange the result of current calculation. Each processor need to send its result to all the other processors, also each of them need to be responsible for receiving the results from all the other processors for the next stage of computation.
4. Synchronousing all the processors to start the next step will be set at the end of global communication.
5. Finally the root processor will take the responsibility for accumulating, selecting and saving the results.
Following are the sample single-chain(serial) pseudo-code; and the correspond duel-chain (parallel) pseudo code that corresponds to the algorithms we just introduced:
single-chain(serial) pseudo-code

duel-chain(parallel) pseudo-code
