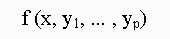 , and are interested in obtaining characteristics of the marginal
density
, and are interested in obtaining characteristics of the marginal
density[Index][Previous-Abstraction] [Next-Solution]
Computer-intensive algorithms, such as the Gibbs sampler, have become increasingly popular statistical tools, both in applied and theoretical work. The continuing availability of inexpensive, high-speed computing has already reshaped many approaches to statistics.
The Gibbs sampler enjoyed an initial surge of popularity starting with the paper of German and Geman(1986), who studied image-processing models. The roots of the method, however, can be traced back to at least Metropolis, ROsenbluth, Rosenbluth, Teller, and Teller(1953), with further development by Hastings(1970). More recently, Gelfand and Smith(1990) generated new interest in the Gibbs sampler by revealing its potential in a wide variety of conventional statistical problems. [George 1992]
Gibbs Sampler is a technique for generating random variables from a (marginal) distribution indirectly, without having to calculate the density. Through the use of Gibbs Sampler, we are able to avoid difficult calculations, replacing them instead with a sequence of easier calculations. It is also extremely useful in classical calculations [Tanner(1991) examples]. Furthermore, this calculational methodology has also had an impact on theory. By freeing statisticians from dealing with complicated calculations, the statistical aspects of a problem can become the main focus.
Suppose we are given a joint density 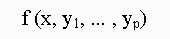 , and are interested in obtaining characteristics of the marginal
density
, and are interested in obtaining characteristics of the marginal
density
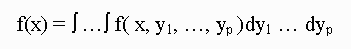 (1)
(1)
such as the mean or variance. Perhaps the most natural and strightforward approach would be to calculate f(x) and use it to obtain the desired characteristic. However, there are many integrations are extremely difficult to perform, either analytically or numerically. In such cases the Gibbs sampler provides and alternative methods for obtaining f(x).
Rather than compute or approximate f(x) directly, the Gibbs sampler allows us effectively to generate a sampler X0, ..., Xm ~ f(x). By simulating a large enough sampler, Gibbs sampler can calculate the mean, variance, or any other characteristic of f(x) to the desired degree of accuracy. So that we are able to avoid calculating integrals like (1), by replacing them with a sequence of one-dimensional random variable generations as (3).
Here we first explore the Gibbs sampler in the two-variable case. Staring with a pair of random variables (X, Y),the Gibbs sampler generates a sample from f(x) by sampling instead from the conditional distributions f(X|y) and f(y|x). This is done by generating a "Gibbs sequence" of random variables
 (2)
(2)
The initial value 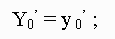 is specified,
and the rest of (1) is obtains iteratively by alternately generating values from
is specified,
and the rest of (1) is obtains iteratively by alternately generating values from
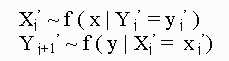 (3)
(3)
Under reasonable general conditions, the distribution of  converges to f(x) as
converges to f(x) as 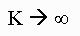 . Thus, for k large enough, the final observation in (1),
. Thus, for k large enough, the final observation in (1), 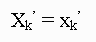 , is effectively a sample point from f(x).
, is effectively a sample point from f(x).
In the Gibbs sequence, after the initial value  is specified, the rest of values are obtained iteratively. Therefore, every
value except for initial
is specified, the rest of values are obtained iteratively. Therefore, every
value except for initial  , is calculated
on the basis of the previous value. The amount of calculation is increasing rapidly
with repect to the length of sequence, the volume of data set and the Intergral's
dimensions.
, is calculated
on the basis of the previous value. The amount of calculation is increasing rapidly
with repect to the length of sequence, the volume of data set and the Intergral's
dimensions.
Suppose it takes the same amount of time (t) to calculate every variable over a unit volume of the data, let Tcomputation be the total computation time, V be volume of the data, M be Intergral dimension and K be the length of sequence, then we have the following equation:

As we can see that the Integral's dimension, the data volume, and the length of sequence will drastically influence the whole Gibbs sampler's comuptation time.